Quá nhiều vấn đề với sự tương quan
Hôm đó là chiều thứ Sáu và sếp của bạn nói rằng dữ liệu đã được cung cấp sớm một cách đáng ngạc nhiên – chỉ trong vòng 4 tuần. Đây chính là mảnh ghép còn thiếu cho mô hình dự đoán của bạn. Bạn rất hào hứng nhưng cũng đôi chút lo lắng vì bạn biết rằng việc tiếp theo phải làm là: khai phá dữ liệu. Tất cả 45 cột. Công việc này sẽ ngốn của bạn hàng giờ đồng hồ nhưng bạn biết nó hoàn toàn xứng đáng vì nếu không hiểu gì về dữ liệu bạn sẽ như mò kim đáy bể vậy.
Bạn tự hỏi: có mối quan hệ nào giữa các cột với nhau?
Để trả lời câu hỏi này, bạn có thể lại phương thức cổ điển quen thuộc: tính ma trận tương quan (corr. Matrix) và xem liệu có mối quan hệ nào đặc biệt không. Mỗi khi bạn tìm thấy mối quan hệ giữa hai cột nào đó, bạn dành thời gian để vẽ một biểu đồ phân tán (scatterplot) của hai cột đó và xem liệu bạn có thể rút ra thêm được gì không. Hi vọng là bạn có thể nhưng đa số trường hợp thì không vì bạn thậm chí còn chẳng hiểu những cột đó có ý nghĩa gì ngay từ ban đầu rồi. Nhưng chúng ta sẽ đề cập vấn đề này trong một bài viết khác.
Sau khi quan sát ma trận tương quan, bạn tiếp tục công việc và không hề biết bạn đã bỏ lỡ điều gì (thật đáng ngại).
Hãy dành chút thời gian để xem lại về sự tương quan. Một giá trị nằm trong khoảng -1 đến 1 và chỉ ra liệu có hay không một quan hệ tuyến tính mạnh (strong linear relationship) – dù theo chiều thuận hay nghich. Mọi thứ đều ổn. Tuy nhiên, có rất nhiều quan hệ phi tuyến mà sự tương quan không thể phát hiện ra được. Ví dụ, dạng sóng hình sin, đường cong bậc hai hay một hàm bí ẩn. Các trường hợp này hệ số tương quan sẽ bằng 0, và kết luận rằng: “Chẳng có mối quan hệ nào ở đây”. Ngoài ra, sự tương quan chỉ được sử dụng với các cột dữ liệu ở dạng số (numeric). Vì vậy, chúng ta sẽ bỏ qua hết các dữ liệu phân loại (categorical). Trong dự án gần đây của tôi, hơn 60% các cột có kiểu dữ liệu phân loại. Và tôi sẽ không chuyển đổi dữ liệu vì chúng không có thứ bậc và OneHotEncoding sẽ tạo ra một ma trận có kích thước lớn hơn cả số nguyên tử trong vũ trụ.
Bạn cũng đã biết rằng ma trận tương quan có tính đối xứng. Do đó về cơ bản chúng ta có thể ném một nửa đi. Tuyệt, chúng ta giảm bớt được chút công việc rồi đó! Đúng không nhỉ? Đối xứng nghĩa là tương quan của A và B bằng tương quan của B và A. Tuy nhiên, các mối quan hệ trong thực tế hiếm khi nào đối xứng. Thường thì, quan hệ là bất đối xứng. Đây là một ví dụ: Lần cuối tôi kiểm tra, mã bưu chính của tôi là 60327 giúp người ta có thể biết rằng tôi đang sống ở Frankfurt, Đức. Nhưng khi tôi chỉ nói cho họ về thành phố, họ thường chẳng bao giờ suy ra được chính xác mã bưu chính cả (Mã bưu chính của một thành phố thường là một khoảng giá trị, ví dụ như Hà Nội sẽ là từ 10000-14000 chứ không phải là một giá trị chính xác duy nhất).
Một ví dụ khác: một cột dữ liệu với 3 giá trị phân biệt sẽ không bao giờ có thể dự đoán chính xác một cột khác với 100 giá trị phân biệt. Nhưng điều ngược lại thì có thể. Rõ ràng, bất đối xứng là một phần rất quan trọng vì chúng rất phổ biến trong thực tế.
Nhận thấy những thiếu sót của tương quan, tôi đã bắt đầu suy nghĩ: liệu chúng ta có thể làm tốt hơn?
Các yêu cầu: Một ngày nào đó của năm ngoái, tôi đã mơ về một điểm số có thể nói cho tôi biết liệu có bất cứ quan hệ nào giữa hai cột – bất kể quan hệ đó là tuyến tính, phi tuyến, quan hệ gaussian hay quan hệ ngoài hành tinh đi chăng nữa. Đương nhiên, điểm số đó sẽ bất đối xứng vì tôi muốn tìm ra mọi mối quan hệ kì lạ giữa thành phố và mã bưu chính. Điểm số sẽ là 0 nếu không có quan hệ nào cả và bằng 1 nếu có một quan hệ hoàn hảo. Và để cho mọi thứ tuyệt vời hơn, điểm số có thể xử lý cả dữ liệu dạng số và dữ liệu phân loại. Tóm lại: một điểm số bất đối xứng, không phụ thuộc kiểu dữ liệu, dự đoán mối quan hệ giữa hai cột, có giá trị từ 0 đến 1.
Tính Điểm số khả năng dự đoán (Predictive Power Score – PPS)
Trước tiên, không tồn tại duy nhất một cách để tính PPS. Thực tế là, có rất nhiều cách có thể tính điểm số khả năng dự đoán thỏa mãn các yêu cầu nêu trên. Vì vậy, hãy nghĩ về PPS như là đại diện cho một họ các điểm số.
Giả sử chúng ta có hai cột và muốn tính PPS của A dự đoán B. Trong trường hợp này, chúng ta coi B là biến mục tiêu và A là thuộc tính duy nhất. Giờ chúng ta có thể tính cross-validated Decision Tree và tính một ma trận đánh giá phù hợp. Khi mục tiêu là biến số học, chúng ta có thể sử dụng Decision Tree Regressor và tính Trung bình sai lệch tuyệt đối (MAE). Khi mục tiêu là biến phân loại, chúng ta có thể sử dụng Decision Tree Classifier và tínhF1 có trọng số. Bạn cũng có thể sử dụng các cách đánh giá khác như ROC nhưng tạm gác lại chúng sang một bên đã vì chúng ta gặp một vấn đề khác:
Hầu hết các ma trận đánh giá đều vô nghĩa nếu bạn không so sánh chúng với một kết quả cơ sở
Tôi đoán bạn đã hiểu tình huống này: bạn nói với bà rằng mô hình mới của bạn có điểm F1 là 0.9 và chẳng hiểu sao bà có vẻ không hài lòng giống như bạn. Thực chất, bà đã rất sáng suốt vì bà chưa biết liệu đã có ai đạt được điểm “0.9” chưa hay bạn là người đầu tiên đạt điểm số cao hơn 0.5 sau rất nhiều cố gắng trước đó. Do đó, chúng ta cần phải “chuẩn hóa” điểm đánh giá của mình. Và bạn sẽ chuẩn hóa điểm như thế nào? Bạn định nghĩa một giới hạn trên và một giới hạn dưới rồi đặt điểm của bạn vào. Vậy giới hạn trên và dưới nên để như thế nào? Hãy bắt đầu với giới hạn trên vì thường nó dễ hơn: điểm F1 tuyệt đối là 1. Điểm MAE tuyệt đối là 0. Bùm! Xong. Thế còn giới hạn dưới thì sao? Thực ra, chúng ta không có đáp án đúng cho mọi trường hợp.
Giới hạn dưới phụ thuộc vào ma trận đánh giá và bộ dữ liệu của bạn. Nó là giá trị mà một mô hình dự đoán đơn giản có thể đạt được.
Nếu bạn đạt được điểm F1 là 0.9 thì nó có thể là vô cùng tệ hoặc thực sự tốt. Nếu mô hình phát hiện ung thư siêu ngầu của bạn luôn đoán “không có bệnh” và vẫn đạt được điểm 0.9 cho bộ dữ liệu rất không cân đối đó thì rõ ràng 0.9 không tốt chút nào. Vậy thì, chúng ta cần tính điểm cho một mô hình thật đơn giản. Nhưng thế nào là một mô hình đơn giản? Đối với bài toán phân loại, luôn đoán giá trị hay xuất hiện nhất là một cách khá đơn giản. Với bài toàn hồi quy, luôn đoán giá trị trung vị là một cách khá đơn giản.
Hãy cùng quan sát một giả thiết chi tiết sau:
Quay lại với ví dụ về mã bưu chính và tên thành phố. Giả sử cả hai cột đều là biến phân loại. Đầu tiên, chúng ta muốn tính PPS của mã bưu chính đối với thành phố. Chúng ta sử dụng điểm F1 có trọng số vì thành phố là biến phân loại. Cross-validated Decision Tree Classifier của chúng ta đạt điểm F1 là 0.95. Chúng ta tính điểm cơ sở bằng cách luôn đoán thành phố hay xuất hiện nhất và đạt điểm F1 là 0.1. Nếu chuẩn hóa điểm, bạn sẽ thu được điểm khả nàng dự báo PPS cuối cùng là 0.94 sau khi áp dụng công thức chuẩn hóa: (0.95–0.1) / (1–0.1). Như chúng ta có thể thấy, 0.94 là điểm khả nàng dự báo khá cao, do đó mã bưu chính có vẻ là có khả năng dự đoán tốt đối với thành phố. Tuy nhiên, nếu chúng ta tính điểm khả nàng dự báo PPS theo chiều ngược lại, chúng ta sẽ được điểm PPS gần với 0 vì Decision Tree Classifier không tốt hơn đáng kể so với việc luôn đoán mã bưu chính thường xuất hiện nhất.
Chú ý: công thức chuẩn hóa cho MAE khác với F1. Với MAE thì càng bé càng tốt và giá trị tốt nhất là 0.
So sánh PPS với tương quan
Để có cái nhìn khách quan hơn về PPS và điểm khác biệt với tương quan, hãy cùng quan sát hai ví dụ dưới đây:
Ví dụ 1: Phi tuyến và bất đối xứng
Hãy dùng quan hệ bậc hai điển hình: thuộc tính x là một biến thống nhất nằm trong khoảng -2 đến 2 và biến mục tiêu y là bình phương của x cộng thêm nhiễu. Trong trường hợp này, x có thể đoán y khá tốt vì có một quan hệ phi tuyến, bậc 2 rõ ràng – sau cùng thì đó chính là cách ta tạo ra dữ liệu. Tuy nhiên, điều này không không còn đúng theo chiều ngược lại là y tới x. Ví dụ, nếu y là 4 thì sẽ không thể đoán được liệu x là 2 hay -2. Như vậy, quan hệ dự đoán là bất đối xứng và điểm số nên phản ánh điều này.
Các điểm số trong ví dụ này bằng bao nhiêu? Nếu bạn chưa biết bạn đang tìm cái gì, thì tương quan cũng sẽ chẳng giúp gì được bạn vì tương quan bằng 0 theo cả hai chiều từ x đến y và từ y đến x vì tương quan có tính đối xứng. Tuy nhiên PPS từ x đến y là 0.67, chỉ ra mối quan hệ phi tuyến. Tuy nhiên, PPS không bằng 1 vì vẫn có nhiễu trong quan hệ. Theo chiều ngược lại, PPS từ y đến x là 0 vì không có quan hệ nào để y có thể đoán được nếu chỉ biết mỗi giá trị của y. Điều này giống với quan sát của chúng ta trước đó.
Ví dụ 2: Cột biến phân loại và mô hình ẩn
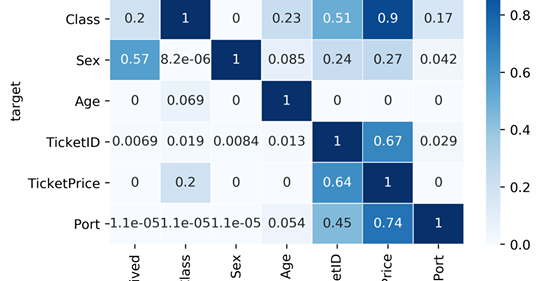
Cùng so sánh ma trận tương quan với ma trận PPS trên bộ dữ liệu Titanic. “Lại là Titanic nữa sao??” Tôi biết, có thể bạn nghĩ rằng bạn đã thấy quen thuộc với bộ dữ liệu Titanic rồi nhưng có thể PPS sẽ cho bạn thêm những góc nhìn sâu hơn.
Hai điều rút ra về ma trận tương quan:
- Ma trận tương quan nhỏ hơn và bỏ qua nhiều quan hệ quan trọng. Đương nhiên, điều đó hợp lý bởi các cột như Giới tính, TicketID hay Port là biến phân loại và không thể tính tương quan với chúng được.
- Ma trận tương quan chỉ ra một tương quan âm giữa Giá vé và Hạng vé ở mức trung bình (-0.55). Chúng ta có thể kiểm tra lại quan hệ này nếu chúng ta nhìn vào PPS. Chúng ta sẽ thấy Giá vé có thể đoán chính xác Hạng vé (0.9 PPS) nhưng chiều ngược lại thì không. Hạng vé chỉ đoán được Giá vé với PPS là 0.33. Điều này hợp lý bởi nếu bạn biết giá vé là 5000$ hay 10000$ thì bạn có thể đoán được đó là hạng vé cao nhất. Ngược lại, nếu bạn biết ai đó ở hạng vé cao nhất thì cũng khó có thể đoán họ trả 5000$ hay 10000$ cho chiếc vé đó. Trong trường hợp này, tính bất đối xứng của PPS lại phát huy hiệu quả.
Bốn nhận xét về ma trận PPS:
- Hàng đầu tiên của ma trận chỉ ra cột dữ liệu độc lập dự đoán tốt nhất cho cột Sống sót là Giới tính. Điều này hợp lý vì phụ nữ thường được ưu tiên trong quá trình cứu hộ. (Chúng ta không thể tìm thấy thông tin này ở ma trận tương quan vì cột Giới tính đã bị bỏ.)
- Nếu bạn để ý cột TicketID, bạn có thể thấy TicketID dự đoán khá tốt một vài cột khác. Nếu đào sâu thêm, bạn sẽ thấy rằng nhiều người có cùng TicketID. TicketID thực chất đại diện cho một nhóm các hành khách cùng mua vé với nhau, ví dụ như gia đình Rossi người Ý. Vậy nên, PPS đã giúp chúng ta phát hiện một mẫu ẩn.
- Điều ngạc nhiên hơn cả khả năng dự đoán của TicketID là khả năng dự đoán tốt của Giá vé đối với nhiều cột. Đặc biệt là: Giá vé dự đoán khá tốt TicketID (0.67) và ngược lại (0.7). Dựa theo tìm hiểu kỹ hơn bạn sẽ nhận ra rằng vé thường có giá nhất định. Ví dụ, chỉ có gia đình Ý Rossi trả giá 72,50$. Đây là một phát hiện vĩ đại! Nó có nghĩa là Giá Vé chứa thông tin về TicketID và về gia đình Rossi. Thông tin mà bạn cần phải có khi cân nhắc lựa chọn thông tin tiềm năng.
- Nhìn vào ma trận PPS, chúng ta có thể thấy một vài đánh giá có thể được giải thích bằng chuỗi nhân quả. (Có phải anh ta vừa nói nhân quả? – Tất nhiên những giả thuyết nhân quả phải được xem xét kĩ lưỡng nhưng điều này vượt quá phạm vi của bài viết.) Ví dụ, bạn sẽ ngạc nhiên tại sao Giá vé lại có khả năng dự đoán khả năng sống sót (PPS 3.39). Nhưng nếu bạn biết rằng Hạng vé ảnh hưởng đến khả năng sống sót (0.36) và Giá Vé dự đoán tốt về Hạng (PPS 0.9), thì bạn đã thấy lời giải thích rồi đó.
Ứng dụng của PPS và ma trận PPS
Sau khi chúng ta đã tìm hiểu về những ưu điểm của PPS, hãy cùng xem chúng ta có thể áp dụng chúng ở đâu trong thực tế.
Chú ý: Có các trường hợp có thể sử dụng cả PPS và tương quan. PPS rõ ràng có những ưu điểm vượt trội hơn tương quan trong việc tìm thuộc tính dự đoán trong dữ liệu. Tuy nhiên, một khi đã tìm thấy thuộc tính, tương quan vẫn là một phương pháp hiệu quả để diễn đạt các quan hệ tuyến tính đã tìm thấy.
- Tìm quan hệ trong dữ liệu: PPS tìm thấy mọi quan hệ mà tương quan tìm thấy – và hơn thế nữa. Do đó, bạn có thể sử dụng ma trận PPS thay thế cho ma trận tương quan để tìm kiếm và hiểu các quan hệ tuyến tính và phi tuyến trong dữ liệu của bạn. Điều này là có thể giữa các kiểu dữ liệu khác nhau, sử dụng một điểm số duy nhất nằm trong khoảng 0 đến 1.
- Lựa chọn thuộc tính: Bổ sung thêm vào cơ chế lựa chọn thuộc tính thông thường của bạn, bạn có thể dùng PPS để tìm ra thuộc tính dự đoán tốt cho biến mục tiêu của bạn. Hơn nữa, bạn cũng có thể loại bỏ các thuộc tính mà chỉ tăng thêm nhiễu cho mô hình. Những thuộc tính đó đôi khi vẫn có điểm cao trong ma trận độ quan trọng của các thuộc tính. Thêm vào đó, bạn có thể loại bỏ các thuộc tính có thể được dự đoán bởi các thuộc tính khác vì chúng không bổ sung thêm thông tin mới (Đa cộng tuyến). Bên cạnh đó, bạn còn có thể đánh dấu các cặp thuộc tính dự đoán tốt lẫn nhau trong ma trận PPS – bao gồm các thuộc tính tương quan mạnh và cả những quan hệ phi tuyến nữa.
- Phát hiện rò rỉ thông tin: Dùng PPS để phát hiện thông tin rò rỉ giữa các biến – kể cả nếu thông tin rò rỉ là trung gian giữa các biến khác.
- Chuẩn hóa dữ liệu: Tìm cấu trúc thực thể trong dữ liệu thông qua việc dịch ma trận PPS như một đồ thị có hướng. Sẽ khá bất ngờ khi dữ liệu chứa các cấu trúc tiềm ẩn mà trước đó chưa được biết tới. Ví dụ: TicketID trong bộ dữ liệu Titanic thường để chỉ một gia đình.
Tốc độ tính toán của PPS so với tương quan?
Mặc dù PPS có nhiều ưu điểm vượt trội hơn tương quan, nhưng vẫn có một số nhược điểm: nó tốn nhiều thời gian tính toán hơn. Nhưng nó tệ đến mức nào? Liệu nó sẽ tiêu tốn nhiều tuần liền hay chỉ sau vài phút hoặc vài giây? Khi tính toán một điểm số PPS duy nhất sử dụng thư viện Python, thời gian sẽ không phải là vấn đề vì thường nó chỉ tốn 10-500ms. Thời gian tính toán chủ yếu phụ thuộc vào kiểu dữ liệu, số hàng và công cụ được sử dụng. tuy nhiên, khi tính toán toàn bộ ma trận PPS với 40 cột tương ứng với 40*40=1600 phép tính thì sẽ tốn 1-10 phút. Với các dự án và bộ dữ liệu của chúng tôi, hiệu suất tính toán luôn đủ tốt nhưng đương nhiên luôn có cách để cải thiện. May mắn là, chúng tôi tìm thấy nhiều cách để cải thiện tốc độ tính toán của PPS.
Những hạn chế
Chúng ta đã tạo ra nó – bạn đang rất phấn khởi và muốn chia sẻ PPS với đồng nghiệp. Tuy nhiên, bạn biết rằng người ta rất hay phê bình những phương pháp mới. Đó là lý do bạn nên hiểu rõ những hạn chế của PPS:
- Tính toán chậm hơn (ma trận) tương quan.
- PPS không thể được diễn giải một cách dễ dàng như tương quan vì nó không cung cấp thông tin gì liên quan đến kiểu quan hệ đã được tìm thấy. Do đó, PPS tốt hơn trong việc tìm ra quan hệ còn tương quan lại nhỉnh hơn trong việc diễn giải các quan hệ tuyến tính.
- Bạn không thể so sánh các điểm số giữa các biến mục tiêu khác nhau vì chúng được tính theo các ma trận đánh giá khác nhau. Điểm số vẫn có ý nghĩa trong thực tế, nhưng bạn cần chú ý điều này.
- Có một số hạn chế đối với các thành phần được sử dụng. Hãy nhớ rằng: bạn có thể thay đổi các thành phần, ví dụ: sử dụng GLM thay cho Decision Tree hay sử dụng ROC thay cho F1.
- Nếu bạn sử dụng PPS cho việc lựa chọn thuộc tính, bạn nên kiểm tra cả trước và sau khi chọn. PPS cũng không thể phát hiện hiệu ứng kết hợp giữa các thuộc tính đối với cột mục tiêu của bạn.
Kết luận
Sau nhiều năm sử dụng tương quan, chúng ta thật dũng cảm (hay điên rồ?) khi đề xuất một sự thay thế giúp phát hiện các quan hệ tuyến tính hoặc phi tuyến. PPS có thể áp dụng với các cột dữ liệu ở dạng số hoặc phân loại và nó có tính bất đối xứng. Chúng tôi đã cung cấp công cụ tính toán trong một thư viện của Python. Hơn nữa, chúng tôi đã chỉ ra điểm khác biệt với tương quan trong một vài ví dụ và đã thảo luận về một số cái nhìn sâu hơn mà chúng ta có thể rút ra được từ ma trận PPS.
Bài gốc: An open-source alternative that finds more patterns in your data.

Đoàn Ngọc Chiến (dịch giả)
Xin chào mọi người, mình là Chiến, 21 tuổi, hiện đang học khóa Machine Learning tại Funix. Bản thân mình vốn không phải người xuất sắc, nhưng mình biết rằng nếu cố gắng nỗ lực thì vẫn sẽ làm được nhiều điều có ích. Do đó, với sự giúp đỡ của mentor hướng dẫn, mình đã dịch bài viết này. Tuy rằng còn nhiều thiếu sót nhưng vẫn mong sẽ nhận được sự đóng góp của mọi người.
Đoàn Ngọc Chiến, sinh năm 1999, hiện đang là sinh viên năm thứ 3, Viện CNTT, ĐH Bách Khoa HN

Nguyễn Văn Quý (hiệu đính)
Mentor Nguyễn Văn Quý, Trưởng bộ phận Phân tích dữ liệu (từ xa) tại VelaCorp, và là Cộng tác nghiên cứu cho Networks Lab, ĐH Alicante, Tây Ban Nha. Hiện đang làm Ph.D về Quantitative tại ĐH này theo học bổng toàn phần.
Mentor Nguyễn Văn Quý từng có kinh nghiệm công tác là Senior Data Scientist tại Tập đoàn Vingroup và Research Consultant tại WorldQuant.
Các chủ đề nghiên cứu: Học máy, học sâu, xử lý ngôn ngữ tự nhiên, Operations Research, Optimization

FUNiX phối hợp cùng công ty Kalapa trao tặng 10 suất học bổng toàn phần với tổng trị giá 200 triệu đồng cho các sinh viên, bạn trẻ yêu thích và muốn theo đuổi lĩnh vực Data Science/Machine Learning trên toàn quốc. Không chỉ có cơ hội được đào tạo bài bản về một trong hai chứng chỉ Machine Learning, Data Science, các ứng viên nhận học bổng còn có cơ hội thực tập, làm việc về các dự án ứng dụng Data Science và Machine Learning vào giải quyết các bài toán thực tế tại Kalapa và các doanh nghiệp khác do FUNiX kết nối. Đăng ký ứng tuyển tại đây.
